Primary Maths Resources: Length, Area and Perimeter

Confusion over calculating length, area and perimeter can occur at all key stages, but Mike Askew's methods can deepen children's...

Key Stage 1

When first learning about length, the National Curriculum specifies that children should learn how to order things by direct comparison using appropriate language. Pupils then go on to compare and measure objects using uniform non-standard units before they eventually progress to using the standard units of length (cm, m).

It is not difficult to set up simple activities involving direct comparison. We can see which shoelace is the longer of two by stretching them out, lining up one end and comparing the alignment of the other ends. A bag of ribbons of different lengths (and different widths) provides a simple resource for a number of sessions on comparisons.

It is also helpful to give children experience of comparisons that cannot be compared directly. For example, children can draw around their foot and their closed hand, then consider the question:

If one ant crawled around the edge of your foot and another ant crawled around the outline of your hand, which ant would crawl further?

Using thick cotton or thin string (dampened to help it stay in place) children can create proxies for the distances around each outline and make a reasonable comparison of which is longer.

In moving away from direct and indirect comparison towards measuring with units, it is common practice to introduce children to units that are shorter than the object being measured: cubes for the length of a ribbon, or handspans for the length of the mat. There is evidence, however, that children’s understanding of the need to measure and the use of tools for doing this is deeper when they begin by using units that are longer than the object being measured. ‘Secret ribbons’ provides such a challenge.

Secret ribbons

Set up two ‘secret’ ribbons in shoeboxes on opposite sides of the classroom. Ask:

Which hidden ribbon is longer?

If the ribbons are close enough in length for the difference not to be easily discerned by inspection, children can be introduced to the use of a tool that is longer than each ribbon: a stick or wooden rod about a metre in length and a pair of elastic bands. (Children who have not been formally introduced to the standard metre rule can still use them - in my experience they happily accept the instruction to just ignore all the marks.)

Lining up one of the ribbons along the stick, children mark its length by rolling an elastic band on and matching it up with the end of the ribbon. Repeating this with the other ribbon, the two elastic bands not only provide the visual evidence for the longer ribbon but also the basis of an understand of a scale. Similar challenges could involve finding the taller of two towers of bricks, one on the floor and one on a table.

Lower Key Stage 2

Once children can measure an object by matching its length with unit cubes and counting up the total, they can move on to creating a ‘unit cube ruler’. (For example, a strip of paper the same length as 20 cubes with marks showing the position of each cube – which can then be advanced to marking, say, the length of every five cubes.)

In learning about area, children again usually start with counting: initially covering surfaces with unit squares and then creating areas on squared paper. However, the move to finding areas of rectangles using a formula has a more problematic connection to counting squares.

Consider this simple rectangle:

Counting the squares is straightforward and talking about there being four rows of five or five columns of four can make some links to multiplication. But consider this version of the rectangle:

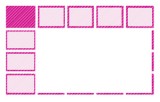
In moving from counting all the squares to using this limited information, a shift has to occur in relation to the (shaded) square in the top left hand corner. When counting individual squares to find the area, this shaded square must be counted once and once only.

But in moving to use multiplication to find the area, this square must be counted twice: once to determine the length of the rectangle and again to find the width. While this may seem obvious to us as adults, it can cause children some confusion.

‘Ripped and torn’ is an activity that can help them move away from counting every square while still supporting that image.

Ripped and torn

Start off by preparing some demonstration rectangles made up of, say, 4 x 4 cm squares. Tear the corner off some of these, hold them up one at a time and invite the children to talk in pairs anddecide how many squares were in the rectangle before it got torn.

Encourage children to use the language of multiplication when sharing their answers with the class:

I could see that it was originally five squares across and four down, so there must have been five times four squares originally.

You should also prepare some rectangles with more than one piece torn off, so that it is not immediately obvious how many squares there are in each row and column.

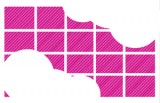
Finally, prepare rectangles where so much has been torn off that finding a unique answer is impossible.

Working in pairs or small groups, the children can prepare Ripped and torn puzzles for each other to solve. They cut out rectangles from squared paper, note down the dimensions of the rectangle (4 by 7) and the area (28 square units). They rip pieces from the rectangle and swap with a partner. Can they write down the same information their partner has recorded about the rectangle?

Bringing the class back together, put up a selection of the data in a table and discuss the relationship between the numbers.

                                                                   

Side 1 (Squares)	Side 2 (Squares)	Area (Squares units)
2	6	12
5	5	25
3	8	24

Upper Key Stage 2

Children have always confused area and perimeter, and will continue to do so! This is partly because there is a counter-intuitive relationship between the two. It seems so reasonable that if the area of a shape gets bigger then its perimeter must also always increase and vice versa.

The activity ‘And another, and another’ challenges children to investigate this relationship and, at the same time, provides plenty of practice in calculating areas and perimeters.

The important thing is that each challenge has to be accompanied by at least three solutions. Finding one solution is usually easy, the second more challenging and the third is the one that pushes thinking on.

Explain to the children that if they are really stuck on finding a third example, they might want to start again and choose an initial rectangle that makes creating three new ones easier.‘Greatest and least’ provides a further opportunity for exploring the relationship between area and perimeter.

And another, and another

Challenge 1
Draw a shape on squared paper that has an area of exactly 20 squares. (It does not have to be a rectangle, but all the edges have to follow the edges of the squares on the paper.)

Find the perimeter of your shape.

Draw another shape which also has an area of exactly 20 squares but which has a longer perimeter.

And another…

And another!

Challenge 2
Draw a shape on squared paper that has a perimeter of exactly 50 units. (It does not have to be a rectangle, but all the edges have to follow the edges of the squares on the paper.)

Find the area of your shape.

Draw another shape which also has a perimeter of exactly 50 units but which has a smaller area.

And another…

And another!

Children can make up similar challenges, either for themselves to work on or to swap with someone else.

Greatest and least

Working in pairs, each child cuts out a rectangle from squared paper. They can choose the dimensions, but to make things manageable you might want to specify that each side of the rectangle should be no longer than 10 units.

Each pair of children puts their two rectangles together to create a shape (not necessarily a rectangle). At least one whole square from each shape must be touching when the new shape is created.

So this is acceptable:

But these are not:

Can children make the shape with the largest perimeter using their two rectangles? What about the shape with the smallest perimeter? How can children be certain that they have found the greatest and least perimeters?

About the author

Mike Askew is Professor of Primary Education at Monash University, Melbourne. Until recently, he was Professor of Mathematics Education at King’s College, University and Director of BEAM.