Primary maths CPD

Paula Stone suggests a process for fine-tuning your mathematical methods...

As such, in this article we will examine progression in calculation strategies, in a bid to ‘MOT’ your maths subject knowledge. (Of course, you could use the structure of these activities to ‘MOT’ any aspect of teaching and learning in the primary classroom.)

What’s the big idea?

To start with you should consider the ‘big ideas’ in calculation. Let’s start with progression – on your own, or with a partner in a different key stage, determine the progression of calculation from Reception to Y6/7 on a time-line such as that below. I’ve already listed two stages to get you started.

When you’ve exhausted your knowledge you could check your answers using the Primary Framework for Mathematics, http://nationalstrategies.standards.dcsf.gov.uk/st rands/34759/34265/110213 (again, bear in mind that this is subject to change with a new government in power).

Next consider everything you need to think about when you teach calculation (you may find it easier to focus on one operation i.e. addition/subtraction/ multiplication/division). Try using a mind map to build up a picture of your ideas. You should think about:

• key vocabulary
• the processes or concepts involved, e.g., the different structures for division; grouping and sharing
• children’s prior knowledge
• connections with other areas of mathematics
• common misconceptions
• models and representations to support learning
• how the examples you choose to use could hinder/enhance learning
• assessment for learning opportunities

It’s important to consider the use of mental and oral mathematics. Not only are mental calculation strategies important in their own right, they also underpin written methods of calculation, so it’s essential that teachers support children’s ability to calculate mentally.

Show your working

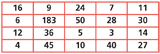Following a look at the ‘big ideas’ of teaching calculation described above, you should test your subject knowledge in the area. Use the number board below to complete the following tasks:

1. Add together the numbers in the third row
2. Find two numbers with a difference of 19
3. Find three numbers that total 37
4. What is the difference between the largest and the smallest number?
5. Find one number that is half of another
6. Increase each number in column one by 9
7. Multiply each number in the top row by 10
8. Double each number in row four
9. Find a product where one factor is 6. What is the other? Find more
10. Multiply each number in the middle column by 7
11. Find two numbers with a difference that is a multiple of 10
12. Divide the largest number by another on the grid so that there is no remainder

What was your initial response to the questions – i.e. did you begin to calculate mentally, reach for pencil and paper or a calculator? Sort your responses into groups according to how you worked them out.

Identifying your strategies for solving the questions is important, as it can have a bearing on how you teach calculation skills to children. Consider the following:

1. Did you just add across? Did you partition then add all the tens and then all the ones? Did you look for numbers that added to a multiple of 10?
2. Did you use your 9x tables? Did you use a strategy based on a number pattern? How would you share this with children? What models and images would you use?
3. Did you find two numbers then find the difference to 37? Did you look for numbers that added to a multiple of 10 then add 7? Did ou find a number ending with 7 and add two numbers that make a multiple of 10?
4. Did you count on or count back? Did you use an empty number line?
5. Did you partition in to tens and ones? Did you use known facts to help you?
6. What pattern did you notice? How would you share this with children
7. How many of you added zero? Acknowledging that this is a strategy that will lead to misconceptions later in children’s mathematical knowledge and understanding, how would you explain this to children? What models and images would you use?
8. Did you partition the numbers?
9. What mathematical knowledge are you using here? What would you do to help children understand this mathematical concept?
10. How many of you reached for pencil and paper? Did any of you partition? Use an array?
11. What number pattern did you use to help with this? How would knowing this help children calculate mentally?
12. Did you approximate first/use grouping to help you calculate mentally/use pencil and paper? Did you say the numbers as numbers (quantity value) e.g. ‘How many 3s in 100?’ or are you using the digit value of the numbers, e.g. ‘3 into 1 won’t go’. What are the implications of this on your teaching and on children’s learning?

Of course, most calculations could have been supported using methods such as counting on/back from the largest number; reordering numbers in addition and multiplication (using the commutative law); partitioning; bridging through 10 and multiples of 10; using inverses; finding differences by counting up; adding/subtracting 9/11 etc. by compensating; multiplying/dividing by 10, 100 etc.; and using known facts. Other options include using the associative law (regrouping) – e.g. (16 x 2) x 5 = 16 x (2 x 5) – and using the distributive law (partitioning) – e.g. 12 x 7 = (10 x 7) + (2 x 7).

Final thoughts

Whilst these activities are designed to help you assess your own knowledge, the key aspect is how you teach these skills. So, when it comes to helping children develop their mental calculation strategies, be aware of the strategies they may use. You should draw attention to and model a variety of them in class, and be prepared to make suggestions to help move them on to more efficient strategies.

It’s also helpful to provide opportunities throughout the day to practise number facts (and not just in maths lessons), and to encourage jottings/informal recordings and the use of number lines/hundred number squares to aid children’s understanding.

Models/images designed to support mental calculation methods can be sourced via the Primary National Strategy Framework http://nationalstrategies.standards.dcsf.gov.uk/search/results/%22models+and+images%22

Find out more

Paula Stone is an NCETM Associate and Senior Lecturer, Primary Education at Canterbury Christ Church University. For more advice on teaching maths visit http://www.ncetm.org.uk