Outstanding maths: Proficiency

Becoming a successful mathematician isn't about learning in stages, suggests Mike Askew. Instead, there are a number of core proficiencies.

A major report on learning primary mathematics, published in the USA*, emphasised the importance of ‘mathematical proficiencies’ - aspects of doing mathematics that, taken together, lead to successful learning. More recently, in Australia, with the launch of a National Curriculum, four of these proficiencies - fluency, understanding, reasoning and problem solving - have been identified as key ‘actions’ to underpin the learning of all mathematics.

Although talk of ‘proficiencies’ is less explicit in the UK, these ideas are creeping into the way we talk about teaching and learning mathematics. For example, the recent Ofsted report ‘Good Practice in Primary Mathematics’, emphasises the importance of ‘pupils’ fluency in calculating, solving problems and reasoning about number’ (p. 33)

In this series of articles, I want to look at these mathematical proficiencies, why they are important, and how we might teach in ways that support learners to develop such proficiencies. To start, let’s look at the importance of reasoning in number work.

Reasoning about calculations

What percentage of 10- and 11-year-olds would you expect to be able to calculate 143 – 86 correctly?

And what percentage of 10- and 11-year-olds would you expect to be able to calculate 143 – 86, given the fact that 86 + 57 = 143?

I’m not a mind reader, but I predict you had a higher percentage for the second question than for the first. You may expect almost all children at the end of primary school to be able to answer the second question correctly; after all, they don’t have to do any calculating. Learners simply have to know that addition and subtraction ‘undo’ each other: subtracting 86 from 143 undoes the effect of adding 86 and 57.

It turns out that knowing that addition and subtraction undo each other is not that simple. In a major research project3 colleagues and I carried out at King’s College, London, we assessed around 2000 children towards the end of Y6 on this understanding. Having established with the children that knowing that 20 + 20 = 40 means you can use that fact to answer 20 + 21, teachers presented the learners with 86 + 57 = 143 and then some other calculations that could be answered quickly with little, if any, calculating (for example 57 + 86, or 860 + 570).

Twenty percent of the children in our study could not figure out that 143 - 86 = 57 based on knowing that 86 + 57 = 143. (In case you are wondering, almost 10% of the children did not know that 57 + 86 would have the same answer as 86 + 57 and around 25% did not realise that 860 + 570 = 1430).

Big ideas

For most numerate adults, it is ‘obvious’ that 86 + 57 = 57 + 86 or that subtracting 86 from 143 brings you back to 57. Mathematically, however, these are ‘big ideas’ - big enough for mathematicians to have given them their own names; commutativity and inverses.

Addition and multiplication are commutative:

3 + 7 = 7 + 3
3 x 7 = 7 x 3

Subtraction and division are not commutative:

7 – 3 = 3 – 7
20 ÷ 5 = 5 ÷ 20

Addition and subtraction are inverse operations; the one ‘undoes’ the other. Similarly multiplication and division are inverses.

These big ideas are important because they underpin much of the reasoning that children need to engage with when they meet algebra. Not knowing that a + b = b + a, or mistakenly thinking that x - y = y - x will be major handicaps. As will not appreciating that a x b / b = a. If, at the end of primary school, around a fifth of children do not understand the relationship between addition and subtraction, then they are likely to encounter problems with algebra at secondary school.

The evidence from psychology is that the structure of children’s thinking is essentially the same as that of adults and that it is lack of experience that accounts for children’s thinking being less accomplished, not an inability to reason (see ‘The myth of stages’). This has implications for thinking about progression in mathematics. We need to be asking where in the primary curriculum are the informal origins of later mathematical reasoning and make these links more explicit.

Teaching implications

Some of the actions associated with mathematical reasoning include:

• Explaining thinking
• Deducing and justifying strategies
• Adapting the known to the unknown
• Transferring learning

Reasoning about number sentences can help children engage with these actions. Missing box calculations can provide a way of making this reasoning explicit to young children without needing to go into algebra.

8 + 7 = 7 + [ ]

When first presented with a number sentence like this, some children will calculate to find the answer. They will add eight and seven to get 15, and then work out that they need to add to seven to make it up to 15. But once they get talking about their methods, some children will begin to understand the thinking behind addition being commutative and that themissing number can be found without calculating.

Children can then explore relationships like:

8 + 7 = 8 + 2 + [ ]
8 + 7 = 8 + 10 - [ ]

Images play a powerful role here in supporting children’s reasoning as they can lead discussion round to how to reason through to an answer, rather than simply calculate it.

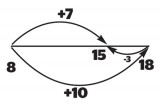Take, for example, 8 + 7 = 8 + 10 - [ ]. Given that 8 + 7 = 15 children will be able to calculate that since 8 + 10 = 18, three needs to be taken off to get 15. Modelling this on an empty number line will help move them away from actually calculating to reasoning about how to ‘compensate’ for the additional amount added.

We can go further and take children out of their calculating comfort zone by working with numbers they cannot easily operate on. Even quite young children can reason around calculations like:

527 + 253 = 253 + [ ]

and move on to examples such as:

527 + 253 = 528 + 200 + [ ]
527 + 253 = 528 + [ ]

Images again play a powerful role here in supporting children’s reasoning.

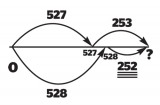Take, for example, 527 + 253 = 528 + [ ]. We can model what is happening here as jumps above and below an empty number line, landing on the same answer.

“How big must the second jump below the line have to be to get us to the same answer? How do you know that?”

Working with colleagues

You could provoke a discussion with colleagues about big ideas like commutativity and inverses by examining the strategies behind working with missing number calculations with numbers that are too big to (easily) calculate.

378 + 245 = 245 + [ ]
378 + 245 = 378 + 241 + [ ]
436 - 157 = 432 - 155 + [ ]
436 + 198 = 436 + 200 - [ ]

As this last example shows, such reasoning is not only powerful for its own sake, but it can help children develop effective mental calculation strategies.

Colleagues could work together on creating similar examples that they think could be used with their classes. A follow-up discussion a week or so later could focus on what the children’s responses revealed about their understanding.

The myth of stages

It is popularly believed that children’s thinking has to have reached a certain ‘stage’ before they can reason mathematically. Such a view was put forward in Piaget’s theory of ‘stages of thinking’ , which included ‘concrete operational’ and ‘formal operational’. Although such ‘stage theory’ is no longer talked about that much, it does still seem to be held that children cannot reason in the same way that adults can.

Researchers now think that Piaget got this part of his theory wrong and that the structures for thinking that we use throughout our lives are very much in place from an early age. Experience is what is needed, not waiting for children to ‘develop’ into a particular form of thinking. Young children can reason about abstract relationships in appropriate contexts. For example, they may not be able to answer 3 / 4 presented ‘out of context’ but can find practical ways to share three chocolate bars between four children.

Another implication is that the need for concrete representations does not diminish as we grow older, although these may be in the form of images and diagrams rather than hands-on materials such as bricks or counters.

Becoming proficient

The everyday use of the term ‘proficient’ carries connotations of a level of expertise. We would not describe someone stumbling through a rendition of Chopsticks as a proficient piano player, having little sense of, say, scales, rhythm or musical notation. But like learning to play the piano, becoming mathematically proficient means engaging in certain actions before one is fully proficient in them. Learning to play the piano does not mean only being introduced to playing a tune once one is fully fluent in playing only scales. Becoming a proficient mathematician means working with all of the proficiencies - fluency, problem solving, reasoning and understanding - from the beginning. And by mathematician, I mean anyone using mathematics in her or his life. Everyone is a mathematician.

What is mathematical proficiency?

In the US report on primary mathematics, adding it up (p.115), the authors argue the importance of five strands of mathematical proficiency:

• Conceptual understanding — comprehension of mathematical concepts, operations, and relations
• Procedural fluency — skill in carrying out procedures flexibly, accurately, efficiently, and appropriately
• Strategic competence — ability to formulate, represent, and solve mathematical problems
• Adaptive reasoning — capacity for logical thought, reflection, explanation, and justification
• Productive disposition — habitual inclination to see mathematics as sensible, useful, and worthwhile, coupled with a belief in diligence and one’s own efficacy.

The entire Adding it up book can be downloaded free from (nap.edu/openbook.php?isbn=0309069955)

About the author

Mike Askew is Professor of Primary Education at Monash University, Melbourne. Until recently, he was Professor of Mathematics Education at King’s College, University.

* Adding it up: Helping children learn mathematics (National Academy Press)