KS1 & KS2 maths: shapes

Wrestle with rectangles, and square up to, er, squares with Mike Askew's cross key-stage conundrums...

These activities are aimed at helping children develop appropriate and accurate language of shapes. A common feature to the activities is the use of a collection of objects: understanding of properties of shape develops as much through looking at the differences and variation between shapes as through looking at the properties of individual shapes.

One aspect to look out for in these activities is children ‘over-defining’ shapes. For example, it’s often the case that children will define a rectangle as a shape with four right-angles and two pairs of equal sides. Actually, just having four right-angles is sufficient information to fix a shape as a rectangle (and gets over the thorny issue of whether or not a square is a rectangle. Squares have four right-angles and so, by definition, are rectangles).

Key stage 1

Behind the wall

I introduce this activity by playing a ‘guess the shape’ activity with the whole class. Preparation involves cutting out a number of 2D shapes from thin card. Using a large book to hide them behind I allow part of the shape to ‘pop’ up from behind the book. Can the children decide what the shape is? When are they certain? As well as using the usual regular shapes I make sure to include less obvious versions of shapes. Not only do these ‘fool’ the children into thinking they know what the shape must be, they also challenge the idea that, say, all pentagons must be regular, or that all trapeziums must look like ‘roofs’.

Next, I give pairs of children a small collection of 2D or 3D shapes, making sure that there are matching pairs of each shape. They find a book to stand up as a ‘wall’ between them. They take it in turns to put four or five of the shapes together to create a design behind the ‘wall’ and hidden from their partner. Can they describe their design so that their partner can re-create it? As well as using the language of naming shapes this helps children to develop their use of positional language. Often their initial instructions can be quite ambiguous (does “Put the triangle on top of the square” mean literally stack them up or position the triangle further away than the square?). I encourage children to sit on their hands when they are describing to stop a hands-on approach to sorting out any communication difficulties.

Lower key stage 2

As children move into KS2, they develop their language to describe 2D and 3D shapes, making more precise use of geometrical terms. Using tree diagrams to sort a small collection of geometrical shapes is a good way both to assess what language children know and to help them develop accurate use of it.

Tree sorts

I introduce the idea of tree sorts by working with the whole class. Inviting four children to the front we play ‘Guess who’. I tell the children I am secretly thinking of one of the four standing at the front, and the class have to ask questions with yes/no answers to find out who I’m thinking of. For example, are they wearing trainers? Or, do they wear glasses? We talk about what a good question is, looking for those that separate the group of four into two groups of two and then split the pairs. Using appropriate questions I draw a tree sorting diagram on the board and then invite children to take turns in secretly thinking of one of the four and have questions directed to them to find out who their mystery person is.

Working in pairs, I give the children a small collection of shapes to create their own tree sorting diagrams. Four or eight shapes is a good number. They draw up their tree diagrams and take it in turns to secretly think of a shape and check their sorting diagram works by getting other children to work through the questions.

Upper key stage 2

Towards the end of primary school children need to be confident in making and drawing with increasing accuracy 2D shapes, and classifying shapes using properties that include angles and pairs of parallel lines. Usually this is done by giving children a collection of shapes and asking them to describe the properties. ‘In the square’ turns this around: by being given properties and having to create shapes children are challenged to think about possibilities (and impossibilities).

In the square

Working in small groups, children are given a large version of this table:

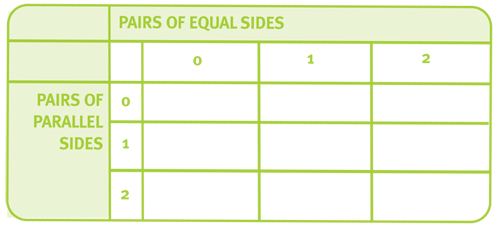
Their challenge is to create quadrilaterals to fill as many of the cells as possible, with the given number of pairs of equal and parallel sides. For example, the centre cell must contain a quadrilateral with exactly one pair of equal sides and one pair of parallel sides (a symmetrical trapezium, for example).

• Can they name their quadrilaterals?
• Are there any cells that can contain more than one type of quadrilateral?

This question focuses the children’s attention on the fact that some quadrilaterals that we give different names to still share common properties. For example, a non-rectangular parallelogram and a rectangle both satisfy the condition of two pairs of parallel sides and two pairs of equal sides.

• What about a square? Does that count as having two pairs of equal sides given that all four sides are equal?

There are some cells that are impossible, for example, a quadrilateral cannot have two pairs of parallel sides and no pairs of equal sides. When the children begin to think some cells have no solutions they usually want confirmation from me that they are right. I resist telling them whether they are correct or not, but bring the class together to share their results and discuss the reasons for why they think quadrilaterals are not possible for some cells.

The main point with this task is not so much the creating of the shapes as working with the children on developing the quality of their ‘arguments’ for why certain shapes belong in particular cells and why some are impossible.

Find out more

Mike Askew is professor of primary education at Monash University, Melbourne and a freelance primary maths consultant. For further information on his work, visit mikeaskew.net