KS1 & KS2 maths: number patterns

Mike Askew challenges children to get their numbers in the right order...

Key stage 1

Children can create and describe two types of number patterns: repeating patterns and growing patterns.

Repeating patterns

Cuisenaire rods or Numicon pieces are good for exploring repeating patterns. If your school does not have these then join inter-locking cubes to make ‘sticks’ one, two, three, four and five cubes long. Use the same colour for all sticks of the same length. The children can prepare sets of these.

• Use the equipment to make a repeating pattern, for example, 1, 3, 5, 1, 3, 5, ... (Figure 1)

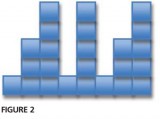Can the children predict what will come next? When they can do this confidently, get them to close their eyes while you secretly hide one of the pieces from the body of the pattern. Can the children say the value of the missing piece? This can be made harder by removing a piece and closing up the gap (Figure 2).

Give the children a collection of the equipment and a paper cup. Working in pairs they create a repeating number pattern. Taking it in turns, one child closes their eyes while their partner puts the cup over one of the number pieces. Can their partner say what is hidden under the cup? Can they record their repeating pattern using pictures or numerals?

Growing and shrinking patterns

On another occasion use one number piece to make a growing pattern, such as that in Figure 3.

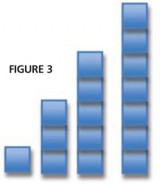As before, can the children predict what the next numbers will be and can they figure out which number is missing when you secretly remove one? In their pairs they can create a growing number sequence using only one number piece and play the ‘under the cup’ game. They can record their number pattern by writing it on a strip of paper. They cut this up into the separate numbers and swap with another pair to try and put each other’s patterns back in the correct order.

• All of these activities can be repeated starting with a large number and creating a shrinking pattern.

Children enjoy making number pattern caterpillars. Provide them with a collection of paper circles. They make one of these the head of their caterpillar and write a simple growing or shrinking pattern rule on the head – + 2, or - 1, for example. They can either choose a rule for themselves or you can give them the rule. They (or you) choose the starting number, and they write this on another circle to create the first segment of the caterpillar’s body. Following the rule they add further sections to the caterpillar until they run out of paper or patience!

“Can the children predict what the next numbers will be and can they figure out which number is missing when you secretly remove one?!”

Lower key stage 2

Working with the patterns of multiples of 2, 5 and 10 provides a solid base for other number patterns. Little and often is a good way to get children familiar with these multiples and whole class chanting and clapping followed by paired work ‘embodies’ these multiples.

Split the class into three, roughly equal groups and name them the twos, fives and tens. Everyone counts in unison, but the whole group has to clap on the numbers that are multiples of their name: the twos clap together on 2, 4, 6, 8, etc., the fives on 5, 10, 15, etc., and so forth. A variation on this is to have everyone stand in a circle. Go round the circle and label every third child ‘two’, the child next to them ‘five’ and the remaining children ‘ten’. As before, the whole class counts out loud together, the children clapping on the multiples of ‘their’ number.

In pairs children can consolidate this further: they face each other and each choose 2, 5 or 10 as their number (a different one each). The count in unison, clapping on the multiples of their number. Children enjoy varying this by taking turns to ‘verbally conduct’ the count. The leader could make the count go faster or slower, louder or quieter, in a squeaky or grumpy voice.

Practise with patterns

Independent work with bags of mixed coins provides further practice in being fluent in these patterns. Prepare bags of 2p, 5p and 10p coins (preferably real rather than plastic). Working in pairs, children empty out the coins, sort them into their values and find the total in the bag by finding the three separate totals and then adding these. This activity can also be reversed: children make up bags of 2p, 5p and 10p coins to exactly total £1 or £2 or whatever. They swap with another pair and check that each other’s bags always contain the same amount.

Back as a whole class, provide some counting that does not always start from low numbers. A good way is to have a tin with lots of coins in it, all of the same denomination, say, 66p in 2ps. Drop coins one at a time into the tin while the children silently keep track of the total. Does everyone agree on the final amount?

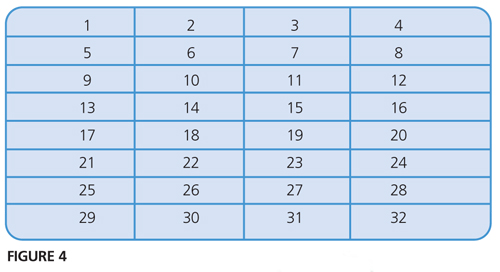
Further work on these multiples can be explored through looking at patterns on the number charts. It is helpful to look at the patterns of the multiples of 2, 5 and 10 on a standard 100 chart, but it’s also interesting to get children to explore the patterns on charts of different widths, say four columns wide or five wide. The children can draw these up themselves on squared paper, to around 50, and then circle or highlight one or more of the multiples. For example, Figure 4 shows the multiples of 5 on a four wide grid. Can they predict which columns larger numbers will be in? Where will 65 be? 100? 165? How do they know? Can they explain in words?

Upper key stage 2

By now children should be beginning to describe the underlying relationship that gives rise to a number pattern. ‘Picture frames’ is a classic investigation to explore this and, for some children, to move into algebra.

Picture frames

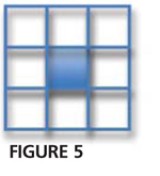Set up the inquiry by talking about making square picture frames by putting unit tiles around a square picture. The smallest possible square picture is 1 x 1 and its frame looks like that in Figure 5.

You need eight tiles to make the frame for a 1 x 1 picture. Ask the children to try and imagine the frame for a 2 x 2 square and agree with a partner on the number of tiles needed. Collect some predictions on the board and invite a child up to draw the tiles for a 2 x 2 picture. Help them to create an image similar to Figure 6.

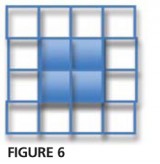Set the children off to either make with square tiles or sketch onto squared paper the frames for 3 x 3, 4 x 4 and 5 x 5 pictures. As the children are doing this encourage them to look for ways of finding the total number of tiles that are quicker than counting them all. Record the size of frame and number of tiles in a table on the board:

                                                                             

Frame	Tiles
1 x 1	8
2 x 2	12
3 x 3	16
4 x 4	20
5 x 5	24

Bring the class together to talk about the total number of tiles: they should find it easy to see that the total goes up by four each time.

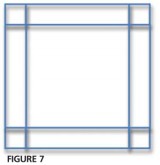
Talk about how they counted the total number for the 5 x 5 picture. For example, someone may have noticed that there are four groups of five tiles that match the sides of the picture plus four more for one at each corner. So the total number of tiles was (4 x 5) + 4 = 24. Draw a diagram that shows this without putting in all the tiles (Figure 7).

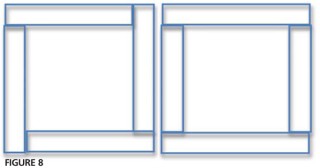What other ways did the children find? For example, someone may have seen the frame as made up of four groups of six, or two groups of 7 and two of 5 (Figure 8). Record these in appropriate fashion:

4 x 6 = 24
(2 x 7) + (2 x 5).

Back in pairs, challenge the children to see if they can figure out how many tiles would be needed to surround a 20 x 20 picture, or even a 100 x 100. Some children may need to add rows to the table, but the challenge of 100 x 100 could encourage them to use one of the shortcuts discussed.

As they complete this, challenge children by telling them that you are thinking of a square picture but you are not going to reveal the size. Can they explain to you how to figure out the number of tiles for the frame? For example, “Take your number and multiply it by 4 and add on 4”. Can the children write down the general rule? If your mystery number is ‘n’, can they write a mathematical sentence?

Find out more

Mike Askew is professor of primary education at Monash University, Melbourne and a freelance primary maths consultant. For further information on his work, visit mikeaskew.net