KS1 & KS2 Maths: multiplication and division

The key to mastering multiplication and division across all the key stages lies in children's ability to spot the corelated calculations

Key Stage 1

Children’s early introduction to multiplication usually begins with a calculation like 4 x 5, which they are taught ‘stands for’ “four times five”. Children may then be encouraged to put out four groups of five counters to find the answer. I suggest (and research backs this up) that rather than starting off with the abstract calculation and then setting up a physical model or diagram to represent it, we are better off starting with simple contexts that can be described and talked about and then represented by a multiplication sentence. In other words, rather than starting from what children do not know (what ‘4 x 5’ means) we begin with something they are familiar with and help them move to the symbolic.

Take, for example, this context problem:

A baker is putting pies on a tray to put in the oven. A tray holds four rows of five pies. How many pies can the baker put onto a full tray?

This context lends itself nicely to children modelling it as a four by five array, either with physical objects or drawings. The discussion would then be around how many pies there are altogether and whether or not anyone had a quick way to find the total that did not involve counting each pie singly. Taking the children’s explanations can lead to introducing the notation of multiplication out of what they saw and did. For example, a child might say that they added five and five and five and five, recorded as 5 + 5 + 5 + 5.

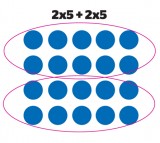Another may say that they saw two groups of 10, each arising from pairs of fives. Marking this up on an image, children can see this recorded as:

2 x 5 + 2 x 5

Even young children will accept the introduction of brackets to help ‘keep things tidy’: (2 x 5 ) + ( 2 x 5).

Similarly, other ‘seeings’ might include 4 + 4 + 4 + 4 + 4. From here it is a short step to introducing 4 x 5 or 5 x 4 as a quick way of recording the repeated additions.

The context of pies on a tray i s not arbitrary. Compare this with, say:

The baker is putting pies into bags. She puts five pies into each bag and fills four bags. How many pies is that?

The model or image that this lends itself to is something like:

While this is fine, because it is less structured it does not lend itself to the variety of ways of seeing, describing and finding the total as the array does. It is also unlikely to lead to a conversation about 4 x 5 being the same as 5 x 4. The equivalence of these two statements is self-evident in the tray of pies, but far from obvious in the context of bags of pies. Rotating the array through a quarter turn clearly leaves the number of pies unchanged, but it is not so immediately obvious that four bags of five must contain the same number of pies as five bags of four.

Other contexts that lend themselves to being modelled as arrays include rows of chairs, square tiles on a floor, and windows made up of small panes. A search on the internet can produce many suitable images that, introduced one at a time over a series of days, will provoke rich conversations about ‘shortcuts’ to counting the total number of items and allow you to drip-feed the notation of multiplication to represent the array.

Lower Key Stage 2

Commonly, division is taught as something that is a development that comes after learning about multiplication. If we introduce multiplication through simple contexts, we can use this to help children understand the close connection between multiplication and division.

Problems such as these help develop this understanding: Jo the grocer is putting apples into bags.

Jo puts nine apples in each bag and fills five bags altogether. How many apples does Jo put into bags?

Jo also bags up some pears. Jo puts nine pears in each bag and has 45 pears to put into bags. How many bags of pears can Jo fill?

Jo is putting oranges into bags. Jo has 45 oranges and five bags. If Jo puts the same number of oranges into each bag, how many oranges are in one bag?

The same context - putting fruit into bags - described in these different ways provides a context to talk about the relationship between multiplication and division. Any multiplication calculation can give rise to essentially two different types of division problems. When Jo is putting pears into bags, the number of pears in each bag is already known - this is a division as repeated subtraction (or quotitioning) problem. The size of the ‘share’ (or quota) is known - nine pears. What we do not know is how many of these ‘shares’ can be made from 45 pears.

In the case of the oranges, the number of shares (bags) is known - five - but we don’t know the number to put into each bag. This is an example of division as sharing or partitioning (the 45 oranges need to be partitioned into five groups, each containing an equal number).

The array can help make clear the connections here.

Upper Key Stage 2

“If three cars have four wheels each, how many wheels is that?”

“If there are four wheels per car, how many wheels would three cars have?”

On the surface these two problems look very similar, but they are subtly different. The first can be thought of as repeated addition, and young children can solve it by modelling the three cars in some way. The second version is more akin to a rate problem, as hinted at by the inclusion of ‘per’. So while both problems can be recorded by 3 x 4 = 12, there is an implicit fourth number in the second problem – the ‘hidden’ one.

• One car has four wheels, how many wheels do three cars have?
• Or 1 is to 4 as 3 is to what?

As children move into upper KS2, we can deepen their understanding of the connection between multiplication and division by introducing them to ratio- or t-tables (as in looking like a T). Our car problem would be represented thus:

                                         

Number of cars	Number of wheels
1	4
3	?

Depending upon the position of the ‘unknown’ in the t-table, we have a multiplication problem or either of the division situations. For example, ‘if a sheet of stickers cost 25p how much would it cost for 18 sheets?’ could be represented as:

                                         

Number of sheets	Cost
1	25p
18	?

Now consider this t-table

                                         

Number of pencils	Cost
1	15p
?	75p

One ‘problem’ that fits with
this t-table could be:

If one pencil costs 15 pence, how many pencils can I buy for 75 pence? Division as repeated subtraction (quotitioning).

                                         

Number of pencils	Cost
1	?
8	£1.20

Now a problem could be:

If 8 pencils cost £1.20, how much does one pencil cost? Division as sharing (partitioning).

Getting children to set out the information in a problem in the form of a t-table can help them be clear about what they have to calculate. But it also provides a flexible tool for helping children figure out the answer. Let’s look at each of these problems again. Filling in additional rows in the t-table can be used to get to the solution.

                                                                                                     

Number of sheets	Cost
1	25p
18	?
2	50p
4	£1.00
8	£2.00
16	£4.00
18	£4.50

(By adding in the cost of two sheets at the end)

                                                                             

Number of pencils	Cost
1	15p
?	75p
2	30p
4	60p
5	75p

(The final entry recognises that doubling again would be too much, and that one more pencil brings the total cost to 75p)

                                                                             

Number of pencils	Cost
1	?
8	£1.20
4	60p
2	30p
1	15p

Roll ‘em up

Of course children still need to practice their multiplication bonds. This is a simple game for doing that (and calculating differences between numbers as well). Children play in pairs and need two dice.

Children roll the dice and use the digits to jot down the smallest two-digit number they can form. This is the target number for that round. For example, rolling at 4 and a 2 they jot down 24. Each child rolls both dice and calculates the product of the two digits. The player whose product is closest to the target number scores a point. The winner is the first to, say, score 10 points.

Player A rolls 3 and 6, that’s a product of 18.
Player B rolls double 5, a product of 25.

Player B scores a point as 25 is closer to 24 than 18 is.

Using 1- 9 dice extends the calculations to 9 x 9.

About the author

Mike Askew is Professor of Primary Education at Monash University, Melbourne. Until recently, he was Professor of Mathematics Education at King’s College, University and Director of BEAM.