KS1 & KS2 maths: multiplication

Give children a firm grasp on multiplication with Mike Askew's hands on lesson plan...

The multiplication square is a powerful image that assists children in memorising multiplication bonds. In this lesson, pupils are asked to construct their own square. This not only helps them to gain an insight into its patterns and structure, but is also a good way for teachers to introduce multiplication as arrays.

I start by getting children to construct a 6 x 6 multiplication square, but only because this is more manageable than going immediately to the 10 x 10 square. However, all the activities here can be extended to the 10 x 10 grid.

Introducing the task

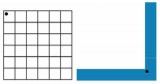Each child needs a blank 6 x 6 grid – 2 cm squares is a good size – and an L-shaped piece of card or heavy paper; the inside edge of the L must be at least 12 cm long. I also prepare large demonstration versions of both resources for the IWB.

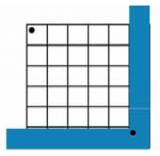
Get the children to mark a dot in the top left hand corner of the grid and also to put a dot in the corner of their L-shape.

I explain to the children that we are going to make rectangles by putting the L-shape onto the grid so that the two dots are always in opposite corners of each rectangle. I demonstrate this and then get individuals to put their L-shape on their grid and describe to the class how they have positioned it. Can the other children follow the instructions and create the same rectangle?

During this time, I introduce the language of rows and columns. In describing the rectangles I adopt the convention of rows first then columns, moving from the extended form of ‘four rows by three columns” to the shortened form of “four by three”. When the children start to use the shortened form I check that “two by six” is two rows by six columns, and not the other way round. I also start to talk about arrays – a three by four array, or a six by one array.

“Russell says his rectangle is five down by four across. That’s five rows and four columns. Now make the rectangle that is four rows by five columns. How is that different to Russell’s rectangle? How is it the same?”

I also discuss whether squares are allowed – do they count as rectangles?

The children work in pairs for a minute or two, taking it in turns to mark off a rectangle and describing it for their partner to make, using the language of rows and columns.

Developing the task

Once I’m confident the children are clear about keeping the L-shape in the correct orientation and are beginning to use the language of rows and columns appropriately, we start to fill in the numbers on the grid.

“Everybody mark off a rectangle that is four rows by three columns. Check with your partner that you have each marked off the same rectangle. Agree with your partner how many small squares there are in that rectangle.”

We agree there are 12 squares in the rectangle and discuss the different ways that the children counted them. Who counted each individual square? Did anyone count in 3s by counting the number in each row? Did anyone use the columns and count in 4s?

I show them to record the total number of squares in the square nearest to the dot on the L-shape.

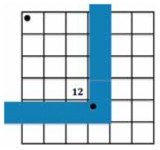“Work with your partner to see if you can find some other rectangles that also contain exactly 12 squares.”

The children quickly find the three by four rectangle and then spot the two by six and six by two.

Finally I set the children off to move the L-shape around and to fill in all the other numbers in the grid. As they are working on this, I look out for children who are counting all the squares in each rectangle individually or filling in the grid in a haphazard manner. I encourage them to look at the patterns that are emerging and to use these to help them predict the number of squares in the rectangles.

Drawing everything together

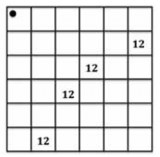When everyone has a completed grid, we work on imagining the arrays and so start to commit multiplication facts to memory. Everyone turns their grid face down on the table. I describe a particular array. Can the children mentally figure out the total number of squares in that array?

“Picture the two by four array: that’s two rows and four columns. Whisper to your partner what you think is the total number of squares in that array. Turn your gird over and use your L-shape to check if you were right.”

Children then work in pairs. One of them marks off an array and describes it to their partner who, without referring to their multiplication square, tries to picture the array and say how many squares must be in it.

Finally, I introduce the multiplication notation. So a four by five array is recorded as 4 x 5 = 20.

Go forth and multiply

Use these extension activities to consolidate children’s learning…

Jigsaw

Get the children to cut a 6 x 6 (and later a 10 x 10) multiplication grid into nine two-by-two squares. Can they put the pieces back together to recreate the grid?

Arrays in arrays

This investigation helps children see how the multiplication facts they have committed to memory can help them to figure out others they have not yet memorized. It also lays the foundation for extending arrays into multiplication of two-digit numbers.

On squared paper, get the children to mark out a five by eight array. They should then explore different ways of dividing this up into two smaller arrays by ruling it off vertically or horizontally. They record the multiplication sentences for each of the smaller arrays and the overall total. Do they get the same total however they divide the array? What about making three smaller arrays? What if they start with a different, larger array?

A quick glimpse

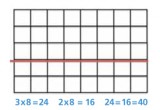One way to encourage the children’s visualization of arrays and to think about the total number of squares they contain is to provide a quick ‘flash’ of a grid on the IWB – long enough for the children to register how many rows and columns the array has, but not long enough to count all the squares. Discuss the ways children figured out the total without being able to count them all.

Find out more

Mike Askew is professor of mathematics education at King’s College London and a freelance primary maths consultant. For further information on his work see http://www.mikeaskew.net