KS1 and KS2 Maths – Place Value

A QUESTION OF VALUE

Understanding place value allows children to unlock large and small numbers, as well as calculating. But it requires a conceptual shift, says Mike Askew…

With only 26 letters, our alphabet allows us to express an infinite number of ideas. Maths is even more efficient – just as many numerical ideas can be expressed with only 10 digits – 0 to 9.

As adults, we are so immersed in a world of numbers, all expressed through place value, that it is easy to forget there is nothing natural about the place value system and that it is a human creation based on a set of agreed conventions. Take, for example, a box of tomatoes. There is nothing about the tomatoes themselves that requires them to be put into groups of 10 (and those groups of 10 into groups of 10 tens). When we do this, we are following a long history of organising quantities.

The distinction between quantities (actual amounts) and numerals (how we represent amounts) is one that we need, as teachers, to keep clearly in mind, else confusion can arise. Many years ago, I overhead a conversation between a teacher and pupil around carrying out the subtraction 264 − 178. It went along the lines of:

T: Can we take eight from four?
P: No
T: So what do we do?
P:We cross out the six and put
five and put a little one by the four.
T:No, we borrow 10 from the 60
to leave 50 and add it to the four
to make 14.

The pupil was not wrong here, but she and the teacher were talking about different things. The pupil’s explanation was at the level of what is literally done – those are the actions carried out on the numerals. The teacher was talking about the actions that would be carried out on the actual quantities – which, in this particular instance, only existed in the teacher’s head. Of course, once you’ve come to understand 264 as two (quantities) of 100, and six of 10, and four ones, it is easy to slip back and forth between quantity talk and numeral talk. But that ease takes quite some time for learners to acquire.

The difficulty is not helped by the fact that we use ‘number’ to refer to both an actual quantity (the number of tomatoes in the box) and the way of recording that quantity (please write down the number of tomatoes). That’s why I’ve been referring to numeralswhen talking about the written symbols. But you turn into an old pedant if you try to be correct about this all the time - please write down the numeral that represents the number of tomatoes.

Conceptually, a big step that children have to make in understanding place value is to perceive groups of 10, or 100, or 1000 and so forth as single entities. And it’s not simple. Imagine you are five and proud of the fact that you can count your fingers and hold them up to show 10, and then someone starts telling you to call them ‘one’.

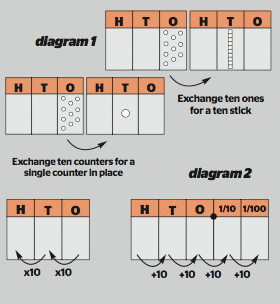
But this process of ‘unitising’ (treating a group as a single entity) is not the only conceptual shift learners need to make. We generally introduce place value through counting, grouping and exchanging: ones are counted out and, when 10 are collected, this group of 10 separate ones is exchanged for a single ‘token’. (This token might still look like a group of 10 if children are using base-ten blocks, or it might be a single token that is denoted as representing ten by its position on a ‘place value board’). see diagram 1

Decimals

Thinking about place value as ‘grouping and exchanging’ is based on additive reasoning (and is how we use and think about place value to add and subtract large numbers). But this is only one way to think about the relationship between digits and their relative position (place). We can also think about place value as a process of scaling up numbers: that a ‘one’ becomes 10 times bigger to become a ‘ten’, and ‘tens’ are scaled up by a factor of 10 to become ‘hundreds’, and so on. This ‘multiplicative’ way of thinking about place value comes into its own with decimal numbers, through reversing the reasoning. If a hundred is scaled down by a factor of 10 to become a ten, and a ten scaled down by a factor of 10 to become a one, then why stop there? The one can be scaled down by a factor of 10 (let’s call the result ‘one tenth’) and that one tenth in turn scaled down to a tenth of its size (and as 100 of those will make a one, so these are sensibly called onehundredths) and so forth). see diagram 2

Large numbers

There are times when the mathematics is actually clearer if you go straight to large numbers, rather than building up gradually to them. Take a numeral (OK, number!) like: 364587322

Read it out loud. It’s not easy and presenting it like this does not help. So we have the convention of presenting it with the digits grouped in threes: 364 587 322 Now we can read it: three hundred and sixty-four million, five hundred and eighty-seven thousand, three hundred and twenty-two The pattern and rhythm of threes is clear: dah hundred and dah-dee-dah million, dah hundred and dah-dee-dah thousand, dah hundred and dahdee- dah. Breaking this down, the five represents ‘hundreds of thousands’, the eight ‘tens of thousands’ and the seven? I’d say that was ‘ones of thousands’, which is why I prefer to call the places hundreds, tens and ones rather than hundreds tens and units (‘units of thousands?)

Place value activities

1 Early years: four blocks

Provide the children with base ten blocks: ones, tens and hundreds. They can each take exactly four of these blocks. Challenge the children to find different numbers between 100 and 1000, all of which can be modelled with exactly four blocks.

This activity can help children realise that a large number, 310 say, can be represented with only a small number of blocks. If children are randomly finding numbers, get them to record each one on a separate slip of paper. Putting these in order can help them see if there are patterns and whether they have missed any possibilities.

2 Middle years: make 100

Working in pairs, children need a pack of playing cards with the picture cards removed. Without looking at the value of the cards, they turn over five. Taking the value of each card, they can use the digit as it is or multiply it by ten. Working together and adding or subtracting the five numbers they create, how close can they get to 100?

For example, the cards turned over are 3, 5, 6, 7, and 9:

90 + 70 − 60 + 5 − 3 = 102 This can also be presented as a whole class challenge. It encourages mental flexibility in working with multiples of 10 as well as encouraging persistence in problem solving.

3 Upper years: order, order

Working in pairs, the first part of this activity involves the children in making a set of 21 cards, each of which displays a different decimal. Nine of the cards have the decimals 0.1 to 0.9 on them. The remaining 12 cards features decimals with tenths and hundreds. Children create these as follows:

1 They mix, face down, the 0.1 to 0.9 cards.
2 They turn one of these cards 57 over and create two new cards – one with a number that’s smaller than the decimal shown and one that is larger then decimal shown (but still less than one). For example, they turn over 0.3 and decide to make 0.27 and 0.56. 3 They repeat step 2 for five more cards.

Using their set of 21 cards, they play the game ‘order, order’. As well as their 21 cards, they need a sheet with 0 and 1 on it and five boxes (each the size of a one of their cards) between the two.

They mix the 21 cards face down. Turning over one card, they have to decide in which of the five boxes they want to place it. Once a card has been positioned it cannot be moved. They turn over a second card: can they place this between 0 and 1 in the correct order? If they can, they put it a box on the sheet. If not, they set it aside. They continue in this way until they have turned over five cards. How many were they able to place in order between 0 and 1? The number of cards correctly placed is their score for round one.

Which pair has the highest cumulative total after, say, five rounds? (At some point, children should swap their cards with another pair.)

The first part of the activity helps develop understanding about ordering decimals with one or two decimal places, while the game consolidates this and requires some strategic thinking.