KS1 and KS2 Maths – numerical reasoning

Numerical reasoning

There are four operations of arithmetic, but what if we were to teach children to think of these as just two types of reasoning? Mike Askew believes we’d create more flexible thinkers…

Imagine two bags of flour, one with a mass of 5 kg and one with a mass of 3 kg.

Before reading on, take a moment to think of the typical ‘compare’ questions that can be asked about these bags of flour.

The sort of questions that pop into most folks’ minds are focused around more than / less than scenarios, with typical problems being:

How many more kg heavier is the 5 kg bag than the 3 kg bag?
How many fewer kg lighter is the 3 kg bag than the 5 kg bag?

It is less often that people come up with ‘how many times heavier / lighter’ questions:

How many times heavier is the 5 kg bag than the 3 kg bag?
How many times lighter is the 3 kg bag than the 5 kg bag?

Note that the numbers here contribute to these latter problems being less obvious. Given a 6 kg bag and a 3 kg bag, we are more likely to talk about one being twice as heavy as the other, or the lighter bag being half as heavy as the other. The ‘messy’ relationship between 5 kg and 3 kg obscures this.

Four operations or two ways of thinking?
In mathematics we often refer to the four operations of arithmetic – addition, subtraction, multiplication and division – but many writers, myself included, think it is more helpful to think about two distinct types of arithmetic reasoning – additive and multiplicative. The bags of flour problems illustrate this difference.

Additive reasoning is based around ‘how much more or less’ and includes situations that can be solved using subtraction. One advantage to thinking about additive reasoning (as opposed to addition and subtraction as two separate operations) is the choice of which operation to use becomes more flexible. 

Figuring out how much heavier an 85 kg adult is than a 7 kg baby could be answered by subtracting 7 from 85, whereas finding out how much heavier the man is than a 79 kg teenager could be worked out by counting up from 79 to 85: different solution strategies, even though both situations are identical.

At first glance, multiplicative problems (situations that can be modelled using either multiplication or division) appear more complicated. Returning to our bags of flour, the 5 kg bag is 1 2/3 times as heavy as the 3 kg bag and, in reverse, the 3 kg bag is 3/5 as light as the 5 kg bag. Whereas, additively, 2 kg heavier and 2 kg lighter appear to be obviously linked, the 1 2/3 and 3/5 may look unrelated – until you think of 1 2/3 as 5/3.

The seeming awkwardness of the numbers in the multiplicative relationship may appear to suggest that this is more difficult than reasoning additively.

Research and curriculum developments do show, however, that even very young learners can reason multiplicatively, given an appropriate context. For example, ‘Milk for the cats’ (see below) is a problem that young learners can solve either practically or through pictures. Talking about their solutions can introduce the language associated with scaling and how the solution can be modelled by the multiplicative relationship 5 x 4.

Distinguishing additive from multiplicative reasoning

It is important for learners to be clear about when to reason additively and when to reason multiplicatively, and to understand that multiplicative reasoning is linked to scaling things up or down (that multiplication is not just repeated addition). For example, if the larger rectangle is a scaled up version of the smaller rectangle, how long is the missing length?

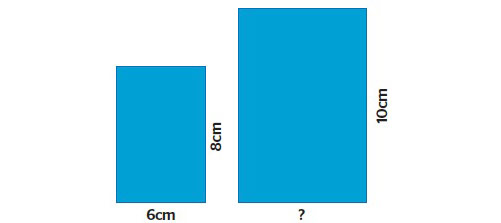
A substantial number of secondary students will, erroneously, reason additively: the side of length 8 cm has been increased by 2 cm to become 10cm, so you also need to add 2 cm to the shorter side, so that it becomes 8 cm. It seems that, for many learners, they develop a stance of ‘when in doubt, add’. What they need to do here is reason multiplicatively: it’s not ‘What do I add to the 8 to make 10?’, but ‘What must I multiply 8 by to make 10?’. That means multiplying 8 by 1.25 (I need one whole 8 and a quarter of 8 to make 10) so to keep everything in proportion, the six must also be multiplied by 1.25, so the longer side becomes 7.25.

‘Making up juice’ (see below) is a context where children’s everyday experience of mixing water and cordial and their informal sense of the fact that it is the proportion of each that affects how strong a drink tastes, rather than the absolute amounts of each liquid, not only helps them to sort out the answers but provides the opportunity to talk about the difference between thinking additively and thinking multiplicatively.

Multiplicative reasoning also comes into play when learning about percentages. Rather than percentages being a completely new idea, these are just a particular type of multiplicative comparison, comparing a part to a whole and standardising the whole to 100. Again, given a suitable context, children can reason informally about this and their informal reasoning can be used to introduce the formal mathematics. One context that works well here is results on a test. Take the following example:

Sam got 18/20 for her maths test and 23/25 on her English test. Sam said she is just as good at maths as she is at English, because she only got two questions wrong in each case.

Asking the children whether or not they agree with Sam’s claim will often prompt them to scale up each test result to make the total number of possible marks equal in each case – 100 is the obvious number and a bridge into percentages is created.

Numerical reasoning activities

In these activities, the emphasis is on reasoning about relationships: getting answers provides a basis for the conversation, but is not the end in itself.

Early years: Milk for cats

This problem is best set up orally – expecting children to read and make sense of it would prove too much. You may need to explain that a cattery is where cats are housed while people go on holiday and getting children to act out what Jo does will help them make sense of what the problem is without giving away how it is solved. Encourage children to draw pictures to help find solutions.

Jo works in a cattery putting our milk for cats.

Every morning Jo has a jug of milk that can fill saucers of milk for 5 cats.

Jo fills the jug from a bucket of milk. From a full bucket of milk, Jo can fill the jug four times.

How many saucers of milk can be filled from the full bucket of milk?

Middle years: The answers are 12

You add two numbers and the answer is 12.
What two numbers might you have added?
Give two different number sentences.

You subtract two numbers and the answer is 12.
What two numbers might you have subtracted?
Give two different number sentences.

You multiply two numbers and the answer is 12.
What two numbers might you have multiplied?
Give two different number sentences.

You divide two numbers and the answer is 12.
What two numbers might you have divided?
Give two different number sentences.

Ask the children to choose one addition, one subtraction, one multiplication and one division sentence from the eight that they have created with 12 as the answer. They should then make up four word problems, one to go with each of their sentences.

This activity encourages children to think about the different types of situations that can be modelled either additively or multiplicatively.

Upper grades: Making squash

Again, this problem is usually best set up orally, with glasses of juice and water just recorded on the board.

Hamsa and Mike were each making up a jug of squash by mixing together water and blackcurrant juice. They wanted their drinks to taste the same, so they measured out the water and juice using glasses. Hamsa made her squash by mixing together 2 glasses of water and 1 glass of blackcurrant juice. Mike did the same, making squash by mixing together 2 glasses of water and 1 glass of blackcurrant juice.

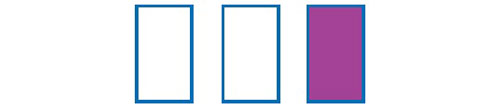
Mike decided that he needed more squash than that so he added to his jug two more glasses of water and two more glasses of juice.

Hamsa said, “Our drinks still taste the same, because in each case there is one more cup of water than juice.”

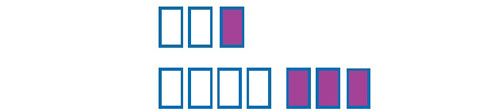
Mike said, “Our drinks still taste the same, because I added two cups of juice and two cups of water.”

Do the children agree with Hamsa and Mike that the drinks still taste the same?

Expect children to have an informal sense that 2:1 will not taste the same as 4:3. The challenge is how to convince someone that these will taste different. One way is to make either the water or juice the same in each case. Hamsa’s 2:1 would taste the same as 4:2. Or 2:1 could be scaled up to 6:3. In each case, this is not the same as 4:3.