Mathematical objects – numbers and shapes – can be described, compared, classified, and analysed by their properties.
Many mathematical ideas are based on classifying – sorting things into groups that share common properties. We happily talk about odd and even numbers, prime and composite numbers, whole numbers and fractions. The world of mathematical shapes is divided into squares and triangles, symmetrical and nonsymmetrical shapes, 2- dimensional and 3-dimensional objects. And we blend together number and shape classifications: there are square numbers, triangular numbers, eight-sided octagons and 12- faced dodecahedrons. It is tempting just to teach different classifications by telling children what the ‘rule’ is in each case (squares have four equal sides and four equal angles). But there is much to be gained by engaging learners in the processes of classifying, rather than simply getting them to commit certain classifications to memory.
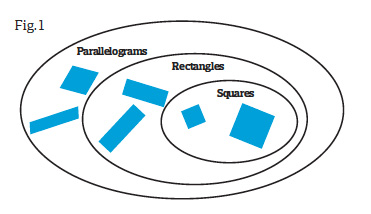
One reason for this is that most mathematical objects belong to more than one classification. A square, for example, is also a rectangle, a parallelogram, a quadrilateral and a rhombus. The number 25 is not only odd, it is also a square number, a multiple of 5, a two-digit number, and so forth. By engaging children in classifying – by taking collections of mathematical objects and asking ‘in what ways are some of these alike?’ and ‘in what ways are some different from others?’, the variety of ways in which mathematicians have chosen to classify things can become clearer.
As the psychologist Ellen Langer has demonstrated, learning can be much more powerful when learners are aware of the conditionality of labelling and classifying: the difference between saying ‘this is a square’ and ‘this could be a square’ can be significant. The definitive – this is a square – makes it more difficult for learners to see that shape as anything but a square. The conditional – ‘this could be a rectangle’ – leaves open the possibility to see the shape as also being a rhombus or parallelogram. The activity ‘Odd one out’ (see overleaf) is one that helps learners develop a sense of this conditionality.
Another advantage of engaging children in the processes of classifying is that it helps them to become aware of the essential properties that define a classification. A classical example here is thinking that a square cannot be a rectangle.
That misunderstanding can arise from defining rectangles as quadrilaterals with four right angles and two pairs of opposite equal sides. That latter criterion – pairs of equal sides – is actually a consequence of the first. Any quadrilateral with four right angles, by necessity, must then have opposite sides that are equal. The clue to defining rectangles is actually in the name – rect (right) angled – a shape with all right angles. (A condition that also means the shape has to be quadrilateral – try making a pentagon with all right angles.) So a square must be a rectangle.
The naming of shapes is based on a mix of properties: ‘rectangle’ emphasises the angle properties of the shape, while ‘equilateral triangle’ emphasises the equality of the lengths of the sides – it could just as easily be called an ‘equiangular triangle’, just as a rhombus is an equilateral quadrilateral, even if that is a bit of a mouthful! The activity ‘Tree sorts’ (see right) helps learners understand there is a certain arbitrariness to the naming of shapes and the interdependence of their properties.
Triangles and quadrilaterals are described, classified, and named based on the properties of their sides and angles. A big idea here is that these shapes are classified by the relative size of their lengths, but the actual size of their angles. In other words all equilateral triangles have three sides of equal length, but these can vary from, say, 1 cm to 1 km. All such triangles also have three angles of equal size, but these are always 60 degrees – no matter how large or small the triangle.
A big idea here is the collection of ‘platonic solids’ – the polyhedra where all the faces are the same and all the vertices have the same number of faces meeting at them. Given these two conditions, there are only five possible solids: the tetrahedron (four faces of equilateral triangles), the sixsided cube (six square faces), the octahedron (eight equilateral triangle faces), the dodecahedron (twelve faces, each a regular pentagon) and the icosahedron (twenty equilateral triangles) c) Numbers can be classified according to properties such as:
We often think of classification as telling us uniquely what a mathematical object is, and what it is not, but it often tells us other things about the object as well. For example, knowing that a number is a multiple of 20 tells us that it is not a prime number, but it also tells us that it must also be a multiple of 2, 4, 5 and 10.
Exploring multiples and the properties of numbers they reveal can introduce learners to the big idea that not all ‘if … then …’ statements are reversible, e.g. If a number is a multiple of 4 then it must be a multiple of 2
Does not imply that:
If a number is a multiple of two then it must be a multiple of four.
Similarly:
If a shape is a square, then it must be parallelogram But it does not logically follow that:
If a shape is a parallelogram then it must be a square. Although currently given less emphasis, Venn diagrams are a great way of visually showing such relationships:
Three children stand in front of the whiteboard, each with a number he cannot see written above his head. (Alternatively, shapes can be drawn above their heads – the game proceeds exactly as described, although obviously the questions asked will be different.) Each child takes it in turn to ask questions about his or her number and the other children can only answer ‘yes’ or ‘no’. If the answer is ‘yes’, he gets another turn. If the answer is ‘no’, the play passes to the next child.
Encourage the children to think about what makes a good question. For example, ‘Is my number 10?’ is not a good question. ‘Is it more than 10?’ is a good question. ‘Is it an even number?’ is even better.
Put four numbers on the board, for example:
18, 21, 23, 25
Working in pairs, the children take each number in turn and have to come up with at least three different reasons as to why that number could be the odd one out. For example: 18 is the odd one out because:
A variation on this is to put up images of four shapes, such as these: (Fig. 2 above)
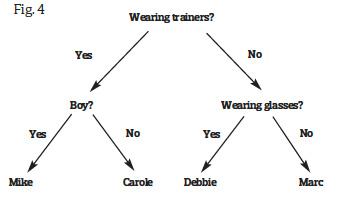
Demonstrate how this activity works with the whole class first. Invite four children to the front. Tell the pupils that you are thinking of a particular child and they have to figure out whom you have chosen. The class has to come up with a question with a yes/no answer that will split the group into two groups of two. For example: ‘Is the person you are thinking of wearing trainers?’ Write the question on the board and draw two paths coming from it, one for ‘yes’ and one for ‘no’. (Fig. 3 )
Without yet revealing whether the answer is ‘yes’ or ‘no’ for the child you have in mind, ask for further questions that split each pair. Record these at the end of each branch, along with names of the children to which the questions lead. Now start at the beginning of your completed question tree and see if the class can use it to work out whom you were thinking of. (Fig. 4)
Working in small groups, give the children a collection of 2- dimensional or 3-dimensional shapes (there can be more than four shapes and children’s questions may not split each collection evenly, but they should try and avoid splitting, say, seven shapes into a group of two and a group of five). The groups make posters of their sorting trees and play ‘What shape am I thinking of?’ with members of other groups to see if their questions work and are unambiguous.
As a whole class, discuss the various questions the groups came up with. Which do the children think are particularly good questions?
In her book Mindful Learning, Ellen Langer makes a strong case for learning that is self-conscious (as opposed to operating on auto-pilot). Part of this rests in the power of the word ‘could’ in promoting deeper learning and more creativity. In a classic experiment, Langer gave adult volunteers, taking part in a test of creativity, a small rubber bone and told them either that it was a dog’s toy (the definite group) or it could be a dog’s toy (the conditional group). All the participants were given a form on which to list possible uses of the bone, and in each case the form had pencil marks on it where it had been used before (Langer gave them these on the pretext of having run out of blank forms). Many people in the conditional group used the bone to rub out the pencil marks – a use for it that did not occur to anyone in the definitive group.
Power Maths – A Child-Centred, ‘Can-Do’ Mastery Teaching Programme for KS1 and KS2
Category: Maths
Fit To Dance Schools From Disney On Ice
Category: Other
‘S!ng Sensational’ And ‘A King Is Born’ – Two Fun New Musical Masterpieces That Children Will Love
Category: Music
Product review: Schofield & Sims Fractions, Decimals & Percentages
Category: Maths
Top tips for differentiation
Ace-Maths
