How to teach fractions in KS1

You’re no more likely to find a ‘half’ in the real world than a tap-dancing fish, which is why it’s important that young learners learn about fractions as relationships, not objects, says Mike Askew...

I’m fascinated by fractions. I admire the even-handedness of halves, appreciate the stable trinity of thirds, and smile at the jostling awkwardness of sevenths. Many folks, however, find fractions about as pleasurable as train spotting, eating tripe or having teeth pulled. For these people, meeting fractions marked the beginning of the end of any affection they felt for maths.

Some people have argued that teaching fractions should be held off until secondary school – not, I think, because there is evidence that primary children cannot understand fractions (there isn’t; they can) but so that children might at least leave primary school with their illusions of liking maths intact.

It is hardly surprising that England’s new maths curriculum’s increased attention to fractions in KS1 sent, if not a tsunami, then at least a ripple of consternation through the primary mathematics education community. Might fractions be a flashpoint in the new curriculum? I think not. But to avoid them becoming so may require rethinking how we currently teach fractions.

What are fractions?

Talking to some teenagers about likes and dislikes in maths, one captured a popular feeling: “I don’t like fractions, ‘cos they’re not real numbers.”

Actually, fractions are real numbers (indeed, to any mathematician, they are Real Numbers), but she was partially correct. Fractions are not real in the sense of you are no more likely to ‘find’ a half, or five-sixths in the real (physical) world than you would a ‘real’ unicorn or a tap-dancing fish. These are all products of the imagination, not descriptions of pre-existing ‘things’. And this is what gives fractions their power. Take the idea of a quarter. I can use this to think about:

The quarter of my cake I’m trying not to eat.
How I’m a quarter of the way through the assignments I’m marking.

That I like salad dressing to be one tablespoon of vinegar to three tablespoons of oil. So if I want to make a large jar, a quarter of it needs to be vinegar.
How the shrub I planted is about a quarter of the height to which it will grow, according its label.

I could go on. The thing to note is that, tempting cake aside, a ‘quarter’ in these examples does not stand for a ‘thing’; it expresses a relationship. You don’t need to know how many assignments, how much dressing I need or what type of shrub I planted, but you can make sense of a ‘quarter’ each time. Even the cake example is, deep down, about a relationship – the relationship between the amount of cake there was to start with and the amount remaining. If I only started off with half a cake, then what would have been a quarter of a whole cake itself become a half. Fractions are tools for thinking about and describing relationships; they are not things or objects. Except, unfortunately, in primary school.

Teaching fractions as objects

Most children initially meet fractions as ‘things’ – half an apple, an eighth of a pizza. That’s where the rot sets in, because one of the things that gets (unintentionally) inferred is that fractions have to ‘look’ right. So this is an OK three-quarters

But this isn’t, because it doesn’t look like three-quarters ‘should’.

Some curriculum documents compound this by insisting on students learning to ‘recognise’ fractions. When I moved to Australia I learned to recognise what a poisonous spider looks like. But when I make sense of how much marking I have left to do, I figure it out – I do not ‘recognise’ that I have done about a quarter.

Later on, children with a sense of fractions as objects have difficulty making sense of things.  Consider this example: ‘A photo of a vase is 14 cm tall, which is two-sevenths of the height of the actual vase. How tall is the actual vase?’ Where is the two-sevenths? It only exists as a relationship, not an amount.

Teaching fractions as relationships

All this may sound like a long way from what six-year-old Jo can deal with. But young children can work with fractions as ways of expressing relationships. The key is to start with the relationships, not the fractions; to work on problems with answers best expressed through the language and notation of fractions.

At heart, there are essentially only two such types of problems: measurement problems and division problems.

This second type is more familiar than the first, so let’s look at it first.

Division problems

Give four children eighth bars of chocolate to share out ‘fairly’ and they can do it, no problem. Give four children three bars of chocolate to share out ‘fairly’ and, though it may be messy, they can do it.

At the end of the first problem, children will know they have two bars each. At the end of second, they may only be able to say that they have ‘some’ chocolate – less than a bar. However, over time, by talking about these amounts, pupils can come to refine their description – three quarters of a bar each. These six-year-olds are doing 3 / 4 = 3/4.

You can also turn the situation round. Talk about going to a party and looking around the room and noticing that there were exactly the same number of boys and girls at the party. Learners investigate how many children might have been at the party. How many boys were there? How many girls were there were and how many children altogether? Rather than that idea of ‘a half’ being limited to one particular image, pupils can reason about a half being dividing one into two equal parts. 

Measurement problems

It is common practice for children to engage in measuring problems like using pencils to measure the desk – which, for instance, might be four pencils long.

It is less common to turn this situation on its head and measure a pencil in terms of ‘desks’, but it’s another opportunity to introduce the language of fractions. The desk is four pencils long; a pencil is one quarter of a desk long.

This may seem contrived, but it is actually the reasoning behind the classic introduction of half an apple. Produce two apples from a bag and these can be described as – obviously – two apples. But that is only because – so subtly that we don’t notice it – we are ‘measuring’ the quantity, the unit being one apple. There are two (of) one-apples. We can change the unit – take pairs of apples. Now we have one (of) a pair-of-apples.

When we cut an apple in half, and the unit of measure is ‘an-apple’, this is half (of) an-apple – or half (of) one-apple.

Fractions can then arise again from problems like:

Jo cut her piece of chocolate into four equal pieces. She only ate three of the pieces. How much of her chocolate did Jo eat?

Introducing equivalence

Ah yes, I hear, but the curriculum says Year 2 learners should meet simple equivalent fractions – isn’t that really too early?

I don’t think so – providing this is introduced through problem solving. Take the Birthday Party Problem.

The Birthday Party

First you need to set up the context for the problem, which I do through introducing twins – Anna and Josh – having a birthday party. The framing story is about the twins going to a pizza parlour for their birthday party and the boys and girls sitting on two separate tables. There were six girls at one table (Anna and five of her friends) and four boys at the other table (Josh and three of his friends). Their father knows that the pizzas are too big for the children to eat one each, so he ordered three pizzas for the girls’ table and two pizzas for the boys’ table. Being good friends, the children shared the pizzas on their table fairly.

After the party on the way home, the twins were chatting about how much they got to eat. Anna said the girls got more to eat because they had more pizzas ordered for their table. Josh said he thought the boys got more to eat because there were not as many boys as there were girls.

What do the children think? Who got more to eat – the boys or the girls?

I want to stress that a problem like The Birthday Party is not intended to treated like a classic word problem – printed out an a worksheet, handed out with children left to muddle through. For children to engage with a problem like this, a lot of time needs to be spent setting up the context, perhaps getting children up to act out being at the different tables. It should be stressed that, when they go off to work on the problem, whatever way they solve it – pictures, diagrams, cutting up circles – is fine. The purpose is to reach a point where everyone is happy that the boys and girls got the same amount of pizza – only at that point can the ideas and notation of fractions be introduced.

What happens is that children solve the problem in different ways and its comparing these different solutions that introduces the idea (and possibly the language) of equivalence. So, for the boys’ table, one solution might be to cut each pizza into four pizzas and hand two pieces to each boy. Another would be to cut each pizza in two, so the boys would only get one piece each.

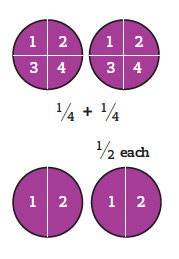
The teaching comes from introducing and using the language and notation of fractions to label and describe what is taking place.

Maths in the real world

Working on creating fractions through solving problems in quite physical ways fits with an increasingly popular view that all of mathematical understandings are, at heart, embodied. That is, abstract though mathematics may appear to be, it arises from our actions, gestures and positions in the world. The writers Lakoff and Núñez provide a engaging introduction to this theory in their book, Where mathematics comes from: how the embodied mind brings mathematics into being (Basic Books, 2001).

About the author

Mike Askew is adjunct professor at Monash University. Now working freelance, Mike teaches, researches and writes about primary mathematics, working internationally with schools and universities. He can be contacted through mikeaskew.net