An attempted assassination becomes the subject of a mathematical mystery your more able pupils will relish...
“Maths is fun!” is the tired refrain that’s often repeated to an unconvinced audience of primary pupils, as if merely saying the words with enough conviction will make them true. Not that enjoyable maths is an oxymoron, it’s just that persuading certain members of the class to rejoice in the innate joy of numbers is a tall order.
When thinking of pupils who turn their noses up at maths, your thoughts may first turn to those who struggle to make progress; but more able children may also be lacking in enthusiasm if lessons are overly formulaic and fail to offer a significant challenge, which is where Detective Inspector Delta steps in.
 D.I. Delta is the chic young investigator who plays the central role in a series of crime stories that open up a range of genuinely engrossing maths investigations - published by Rising Stars (risingstars-uk.com) in association with NACE (National Association for Able Children in Education). The mysteries are presented to pupils as challenge booklets with illustrations more commonly seen in graphic novels than text books, and crime contexts that are neither patronising nor too much like a late night episode of Luther. Deftly written and cleverly engaging, it’s quickly apparent why children are so eager to help D.I. Delta solve her cases by putting their skills of analysis, inference and evaluation to good use.
D.I. Delta is the chic young investigator who plays the central role in a series of crime stories that open up a range of genuinely engrossing maths investigations - published by Rising Stars (risingstars-uk.com) in association with NACE (National Association for Able Children in Education). The mysteries are presented to pupils as challenge booklets with illustrations more commonly seen in graphic novels than text books, and crime contexts that are neither patronising nor too much like a late night episode of Luther. Deftly written and cleverly engaging, it’s quickly apparent why children are so eager to help D.I. Delta solve her cases by putting their skills of analysis, inference and evaluation to good use.
Rising Stars currently offers six D.I. Delta mysteries, each with teacher’s notes - one of which we have here for you to try with your more able pupils. As with all the crime stories, they work equally well as small group tasks, homework, or challenges for an after-school maths club.
On a visit to London, the US President visited 10 Downing Street. While the President was talking with the Prime Minister a shot was fired, narrowly missing the President. D.I. Delta is called to investigate.
She begins to gather information. The Prime Minister and the President had been alone in the meeting room, sitting at a table. The room has a single sash window with bullet-proof glass. At the start of the meeting, through the window, they saw a person outside in the garden. They assumed this person was a gardener.
The President asked for some fresh air, so an assistant was called. The assistant lowered the sash window, leaving a small gap of about 10 cm at the top. While the President and Prime Minister were watching the assistant leave, the person in the garden fired a shot through the partly opened window, before running off. The shot hit the wall, just above where the President was sitting.
US Secret Service agents rushed into the room. Some were sent to try to catch the would-be assassin. The Prime Minister and President move to a safer place and Delta is left alone in the room. She begins her examination by studying the bullet embedded in the wall. She then examines the rest of the scene, and notes that there is no broken glass in the room. She draws a sketch and makes measurements. Her sketch shows the East wall with the window and the opposite West wall containing the bullet.
 Delta is surprised that the bullet came through such a small gap. She decides to work out the angles (to the horizontal) of the highest and lowest paths the bullet could have followed to enter the room.
Delta is surprised that the bullet came through such a small gap. She decides to work out the angles (to the horizontal) of the highest and lowest paths the bullet could have followed to enter the room.
1. What strategies do you think Delta used to work out the angles shown on her sketch(Fig.1)? Use your own strategies to work out angles A and B (the angles to the horizontal) marked on her sketch. You may choose to draw your own accurate drawing or do some calculations to work this out.
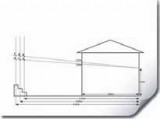 2. The President had been sitting directly opposite the window about 1 metre from the West wall of the room. When standing, the President’s height is 6 foot 1 inch, but when sitting his head is 40cm lower. What do you think might have happened if he had been sitting closer to the West wall… and why?
2. The President had been sitting directly opposite the window about 1 metre from the West wall of the room. When standing, the President’s height is 6 foot 1 inch, but when sitting his head is 40cm lower. What do you think might have happened if he had been sitting closer to the West wall… and why?
Delta goes into the garden to see where the assassin must have been standing when he or she fired the shot. A witness tells her that he saw a person, dressed in green, standing on some steps a short distance from the window. Delta takes more measurements and draws some more sketches. She notices that the steps are directly in line with the window and the bullet. The witness had seen the assassin stand up straight and fire the gun, but could not remember on which step the person was standing. Delta stands on each step and tries to see the bullet through the gap.
To see through the gap in the window across to the bullet in the wall, a person’s eyes must be between the two dashed lines drawn at the top and bottom of the gap (see Fig.2). Delta uses a computer program to find out at what height above ground level the suspect’s eyes must have been. She works out that the heights from ground level of the points a, b, c, d, e and f on her diagram are as follows: a = 1.80m, b = 2.00m, c = 1.81m, d = 2.02m, e = 1.83m, f = 2.05m
3. What information from Question 1 might Delta have used to work out thepositions of a, b, c, d, e and f? How do you think the computer program might have worked out the results? What might you have done to work out these heights?
Delta realises that she needs to measure the height of the steps. Each step is 15cm high.
4. Now work out the distance between the top of the lowest step and points a and b; the distance between the top of the middle step and points c and d; and the distance between the top of the highest step and points e and f. How do you think Delta would have noted exactly how she came to those conclusions about the height of the steps?
Just then the US Secret Service brings three suspects to her. All three were seen running from the scene and all are wearing green. Two are men known to Delta – Fred (known as Fred the Terrible) and Bill (known as Big Bill despite being quite small). The third suspect is Ivy, a female gardener at Downing Street. Delta knows that if she measures the distance from feet to eye-level for each of these suspects, she might be able to work out which was the assassin.
| Name | Distance from feet to eyes |
|---|---|
| Ivor | 186 |
| Bill | 140 |
| Ivy | 163 |
5. Use your own strategies to work out which suspect could have been standing on which step to fire the bullet (assume that the bullet travelled in a straight line). You may choose to draw your own accurate drawing or to do some calculations to work this out. Can you rule out any of the suspects?
Delta now thinks that it must be one of two suspects. To determine which of the two is the assassin, the gun must be found. She guesses that the suspect must have hidden it nearby. After a careful search, the gun is found pushed carefully behind a broken brick in a wall, about 7 feet up. The gun is fingerprinted and the suspect arrested.
 6. Which suspect do you think was the would-be assassin? Produce a report of the investigation and findings and suggest who you would arrest and why. Include an explanation of how you worked out and could prove your findings.
6. Which suspect do you think was the would-be assassin? Produce a report of the investigation and findings and suggest who you would arrest and why. Include an explanation of how you worked out and could prove your findings.
7. With the case solved and the suspect in jail, Delta wonders what they should do to ensure the protection of others in the room in future, if the window is slightly open. How do you think this could be achieved? Delta considers putting up a tall fence so that a person standing on the tallest step cannot see into the room. How high should the fence be? Where would be the best position for the fence? Why doyou think that?

Use the D.I. delta mysteries to:
• Develop higher-order thinking skills, particularly reasoning and logic
• Stimulate speaking and listening around maths problems
• Provide children with a focus for using and applying maths For more information on the complete set of D.I. Delta Mysteries, visit risingstarsuk.com
Pdfs of both the pupil activities and the accompanying teacher’s notes for this instalment of the D.I. Delta Mysteries from Rising Stars are available for download. Visit risingstars-uk.com/delta to get your copy.
Pie Corbett’s bike poems
Topic
Make every lesson an experiment
Cross Curricular
